AGI progress has stalled.
New ideas are needed.
How to Beat ARC-AGI by Combining Deep Learning and Program Synthesis
Deep learning is not enough to beat ARC Prize. We need something more. Mike Knoop and François Chollet lay out a technical approach path via Program Synthesis that just might finally defeat the only AI benchmark that measures our progress to AGI.
After visiting over a dozen top US AI universities, we hosted a live, virtual event on October 24, 2024, to share our university tour content with anyone curious about AGI. You can watch the livestream replay above or read the speaker notes below.
Mike Knoop
Here’s the story we like to tell about artificial intelligence.
Since basically the beginning of the field, researchers have sought to build AI by leveraging their human knowledge and expert insight into intelligence and the brain.
While this was the favored method, it was also pragmatic. Cheap compute did not exist… yet. The cost of compute has been falling consistently 2 orders of magnitude every decade since 1940.
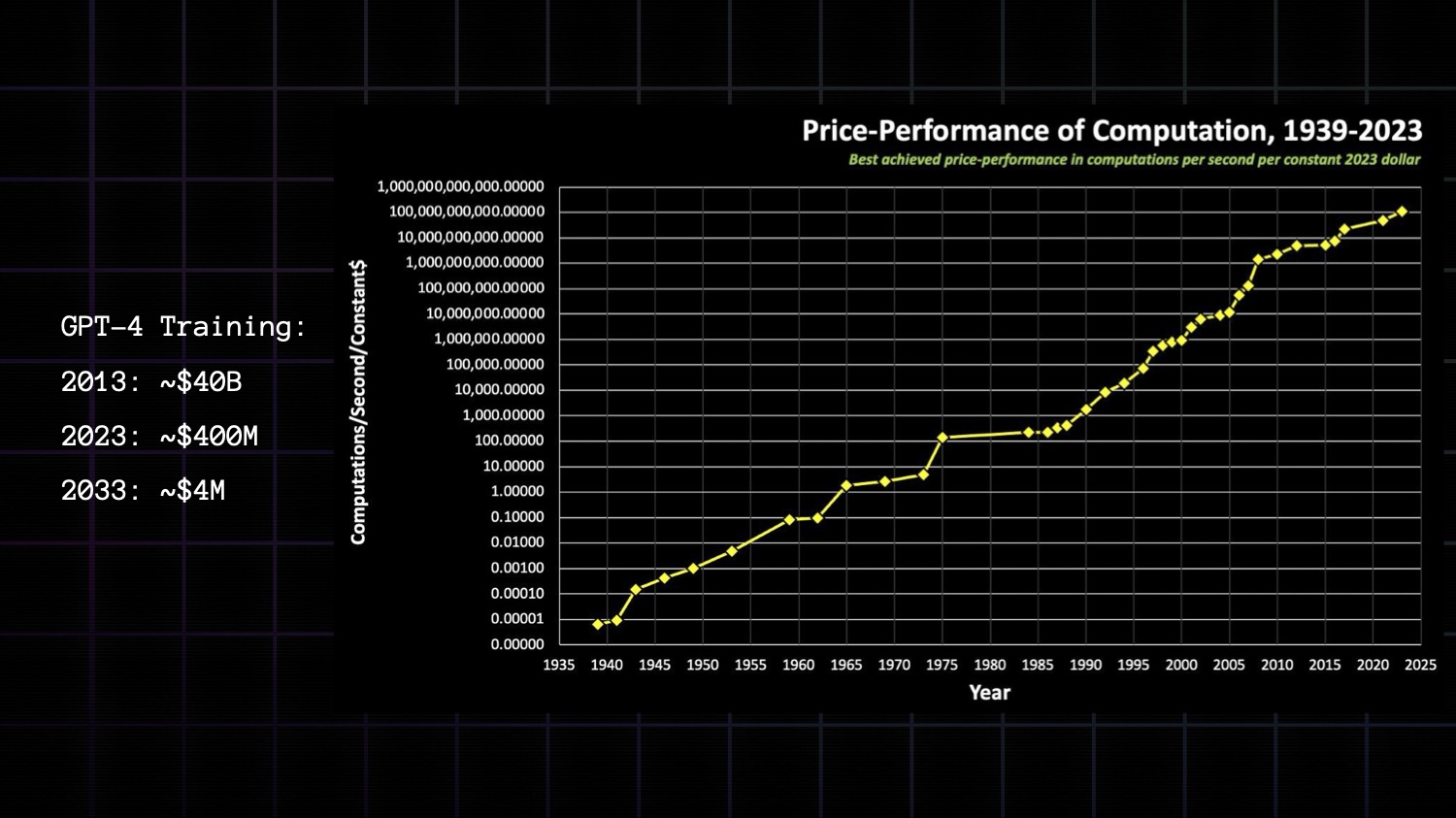
Finally in the 2010s, enabled by the abundance of cheap GPUs, deep learning methods started to work. From ImageNet to the transformer, we started to see general purpose search and learning methods applied to build ever more impressive AI systems that could succeed in previously "impossible" domains like image recognition, games like GO, protein folding, self-driving cars, and even language.
Price-performance of compute continue to scale today and there is no hint they’ll slow down over the next decade.
Using this curve we can even predict GPT training cost (10^26 FLOP model trained in 1 month):
- 2013: ~$40B
- 2023: ~$400M (about right!)
- 2033: ~$4M
Measuring Performance
Language modeling turned out to be even more powerful than most expected. These LLMs started reaching human capability on every AI benchmark we could throw at them.
Moreso, progress on AI benchmarks has been accelerating. These methods empirically work and most of the industry believes they will continue to scale up until we get to artificial general intelligence (AGI).
We like to tell this story because it not only fits the data we have about the last 10+ years of deep learning progress, but the last 80+ years of scaling compute.
But the conclusion that deep learning can scale to AGI assumes a certain definition of AGI – one that is oriented around AI's skill as opposed to AI's ability to learn skill.
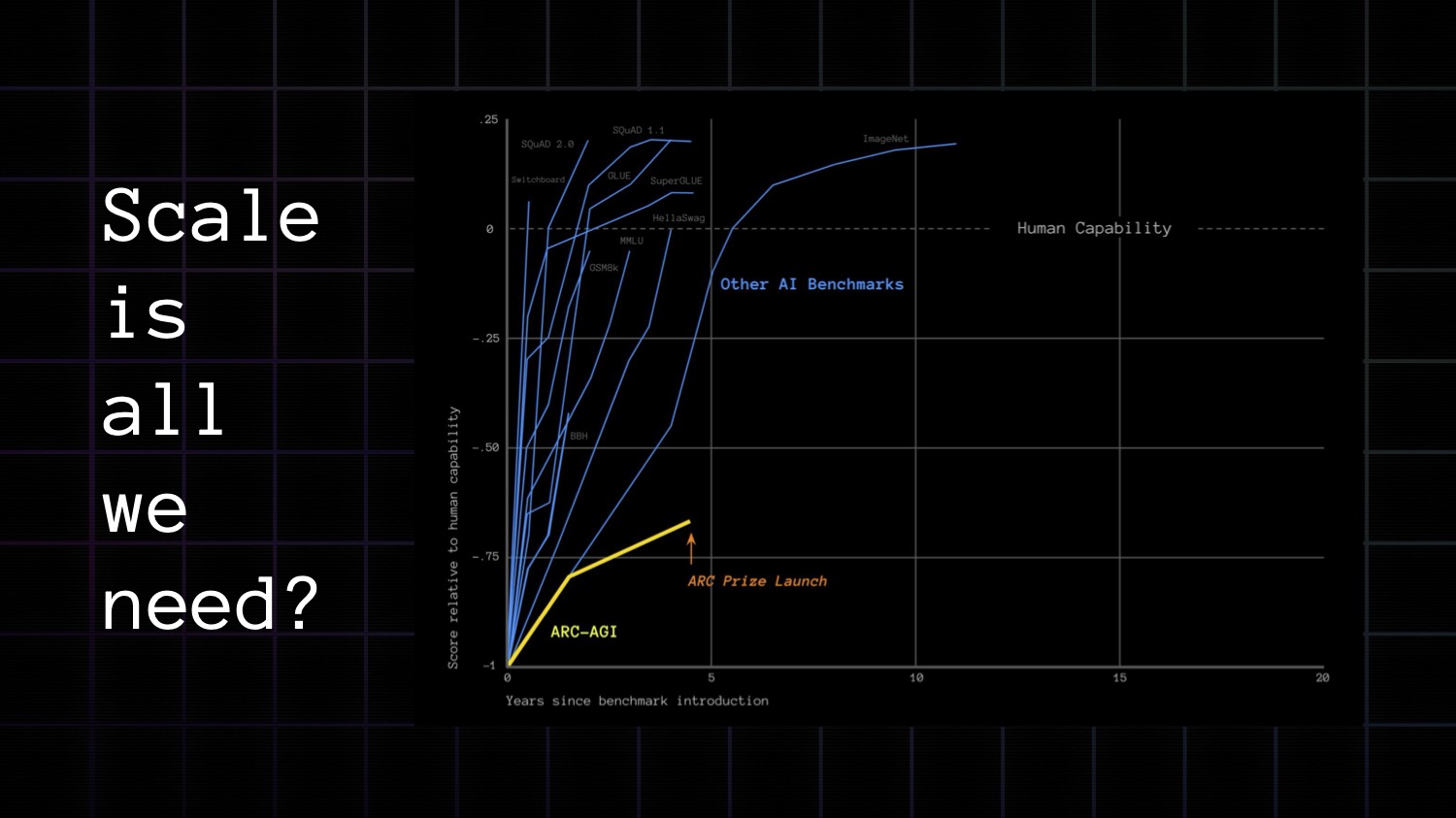
In 2019, François Chollet published the ARC-AGI benchmark to test whether AI systems could efficiently learn skill and apply it to problems it’d never seen before. 5 years later his benchmark remains unbeaten. Heading into June of this year, progress had even been decelerating.
What if scale is not all we need for AGI?
A Novel AI Benchmark
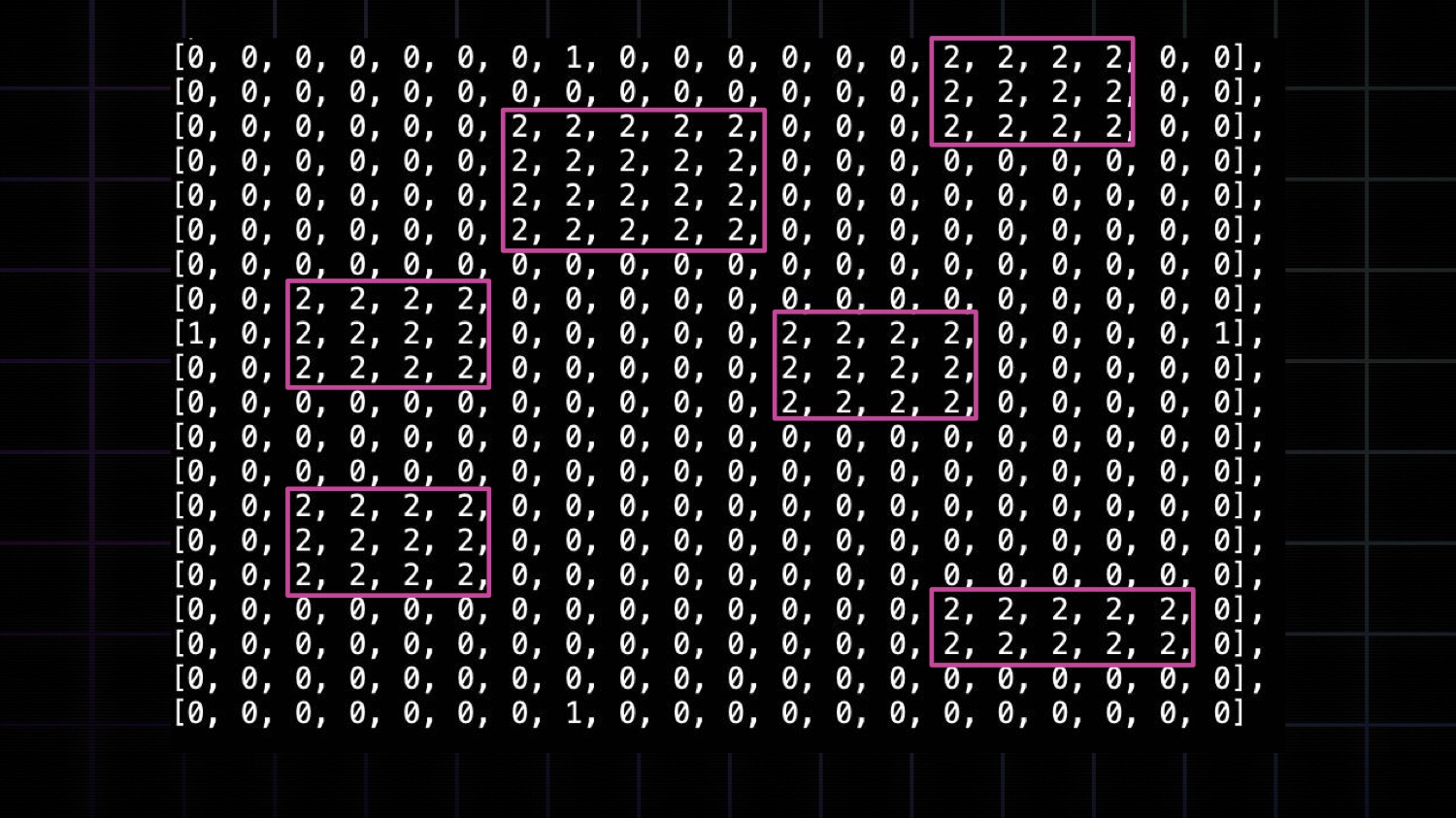
You might be curious what this benchmark is. Show is better than tell, so let's take a look an ARC-AGI task. It's like an IQ test.
The benchmark has hundreds of these puzzles. Each one is unique. The puzzles are designed to be easy for humans to solve. Human testing data even shows that 98% of the ARC private evaluation dataset is solvable by one person.
But today, no AI system can solve ARC.
One common misconception is that ARC-AGI is a visual benchmark. Instead, it's better to think of it as a programming benchmark mapping a 2D array of numbers to numbers.
When I rediscovered the benchmark a few years ago I was surprised it hadn’t been beaten yet.
What makes ARC-AGI so special and resilient?
- Every task is unique and novel. There is no easy way to "cram" for ARC. This is in contrast to how deep learning works by adding more and more training examples into models, effectively memorizing answers and situations.
- ARC tasks only assume a handful of core knowledge priors like basic math, counting, geometry, topology. These are skills you acquire during childhood. ARC requires strong and efficient generalization to compose and abstract from core knowledge on the fly.
- The state-of-the-art is measured on a private evaluation set of 100 puzzles. This helps ensure no one can overfit or contaminate with the answers or solution paths. It increases confidence that a SOTA score on ARC is true progress.
- Solving ARC requires efficiency. You get 2 guesses per task and a limited amount of compute and time for all 100 tasks. Brute force search, which demonstrate skill, is not a demonstration of intelligence.
Unfortunately ARC-AGI has been fairly obscure. I've been surveying AI researchers in the Bay Area for a few years and less than 10% of researchers I meet have heard of it.
ARC's durability suggests we need new ideas to discover AGI. And if that’s true, I believe way more people need to know it exists!
So François Chollet and I decided to launch ARC Prize, a $1M nonprofit competition to beat ARC and open source the solution. It's a grand experiment to test our hypothesis on the largest scale possible. Can frontier AI ideas beat ARC?
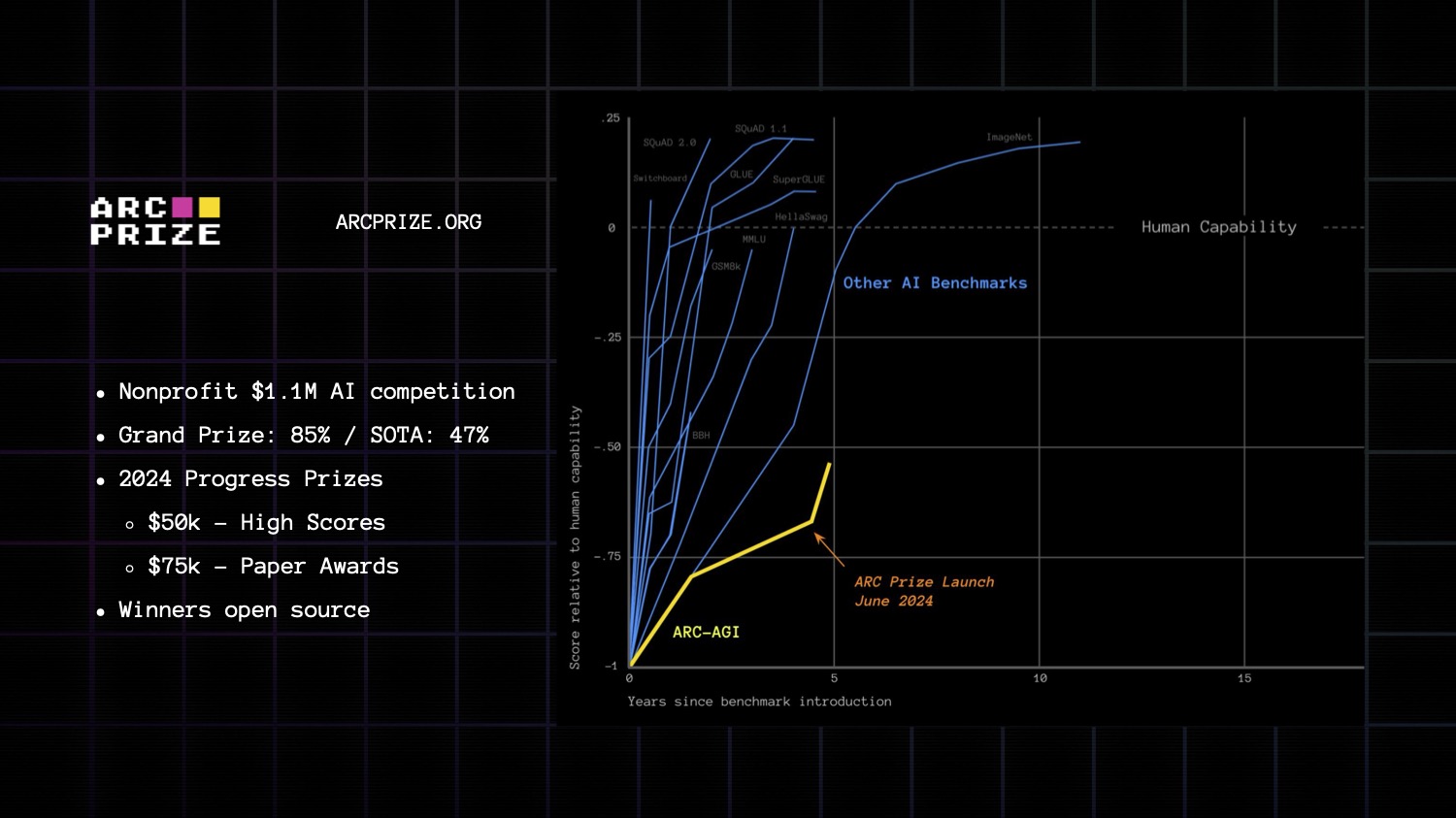
We're over three months into the contest now and we can more confidently answer this question: NO.
The large prize clears the space of low hanging fruit ideas to beat ARC.
This is fairly strong evidence we’re missing something - likely something big, and maybe as fundamental as deep learning itself.
Since launch, we gained 20%+ on SOTA! We're finally seeing some progress as teams apply similar techniques to DeepMind's AlphaProof and OpenAI's o1 model towards beating ARC.
I think it's especially cool that even while AlphaProof and o1 are closed source and we barely got blog posts detailing their architectures, by the end of this year, we expect to open source several re-implementations of these systems driven by ARC Prize.
This progress is promising but also shows we have a long way to go still.
OpenAI's new o1 model in particular is worth better understanding.
Reasoning Models
Released in Sept 2024, OpenAI said that o1 is not just another LLM, instead it represents an entirely new paradigm for scaling AI. When o1 launched, thousands of people asked if it could beat ARC.
We tested it. Here's the result.
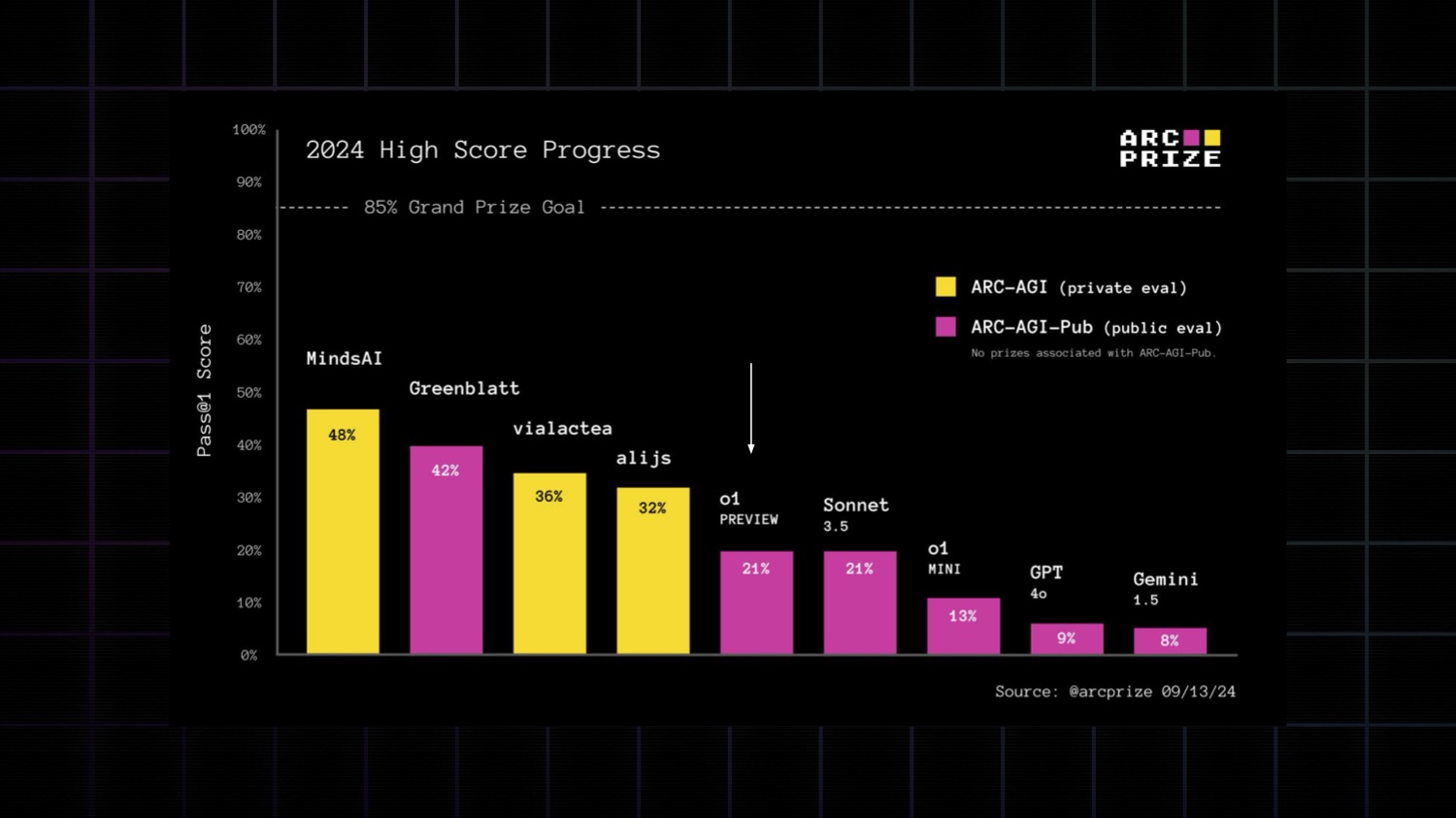
o1-preview scores double what GPT-4o scores and is about on par with Claude 3.5 Sonnet.
Despite it's modest ARC-AGI score, o1 is not just another frontier LLM. It is the biggest genuine generalization improvement in a commercial AI model since GPT-2 launched all the way back in 2019.
o1 fully exploits the "chain of thought" reasoning paradigm (i.e., "lets think step by step") at both pre-train and inference time. At training time, o1 is trained on synthetic "chain of thought" reasoning chains scored formally (in code, math, theorem domains) or informally (using RLHF). At test time, o1 is given additional compute time to search and backtrack over it's chain of thought to find better solutions.
While pre-training continues to improve with more data, this is to be expected given what we know about LLMs already.
The big new story is the test-time compute. OpenAI published a chart showing a log-linear relationship between test-time inference compute and accuracy.
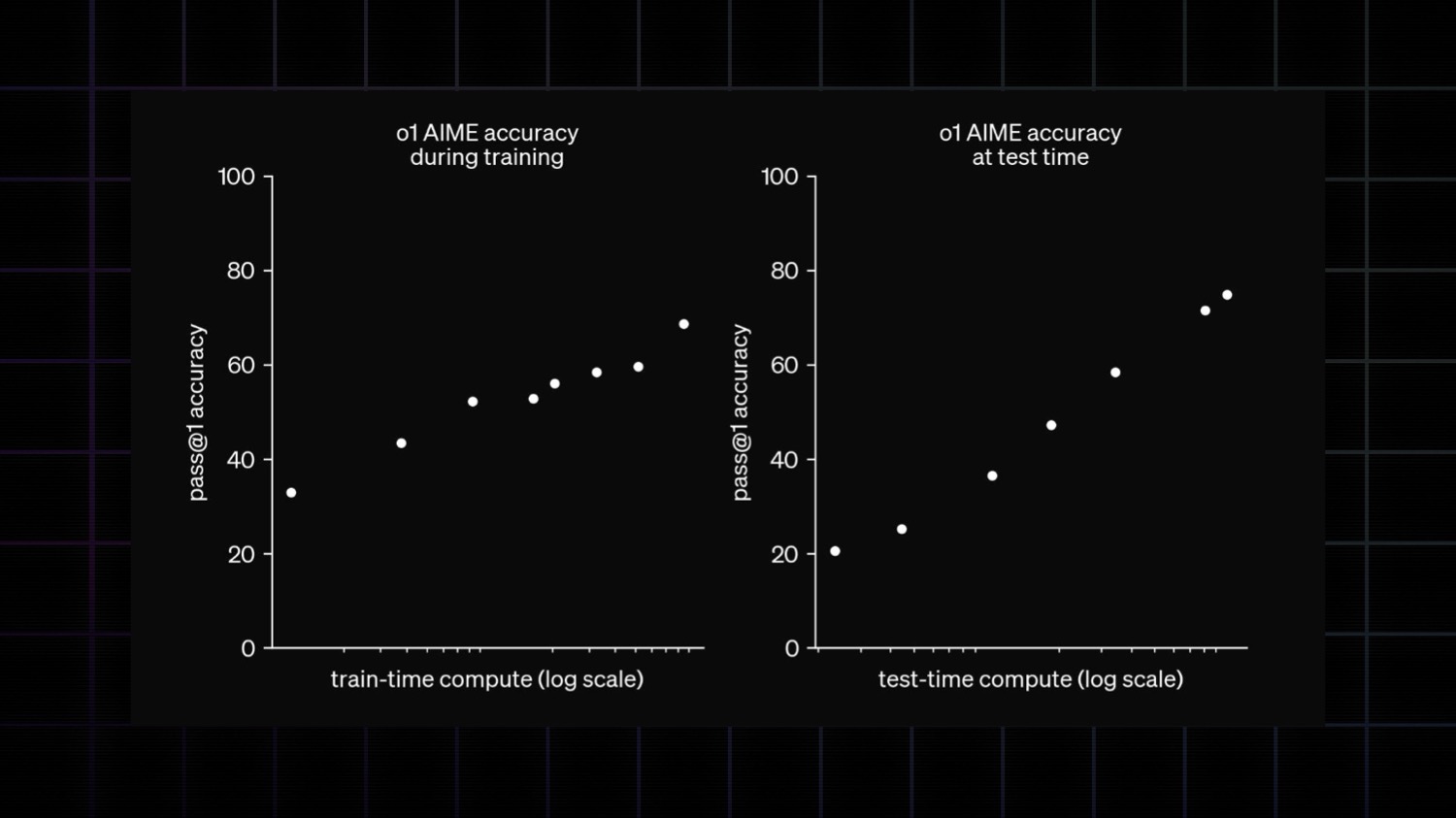
This makes reporting on o1 tricky, and this will become true for every AI system in the future. Single benchmark scores will get more and more deceiving.
OpenAI made an arbitrary product decision to set o1's test-time compute to some amount. Had they allowed less, it would have scored worse. More, more.
This wasn't the first time I'd seen this log-linear relationship in a chart. We saw something similar with ARC Prize just 2 months ago.
It was the top submission on our public ARC leaderboard. That approach found this identical log-linear relationship between accuracy and test-time compute on ARC-AGI.
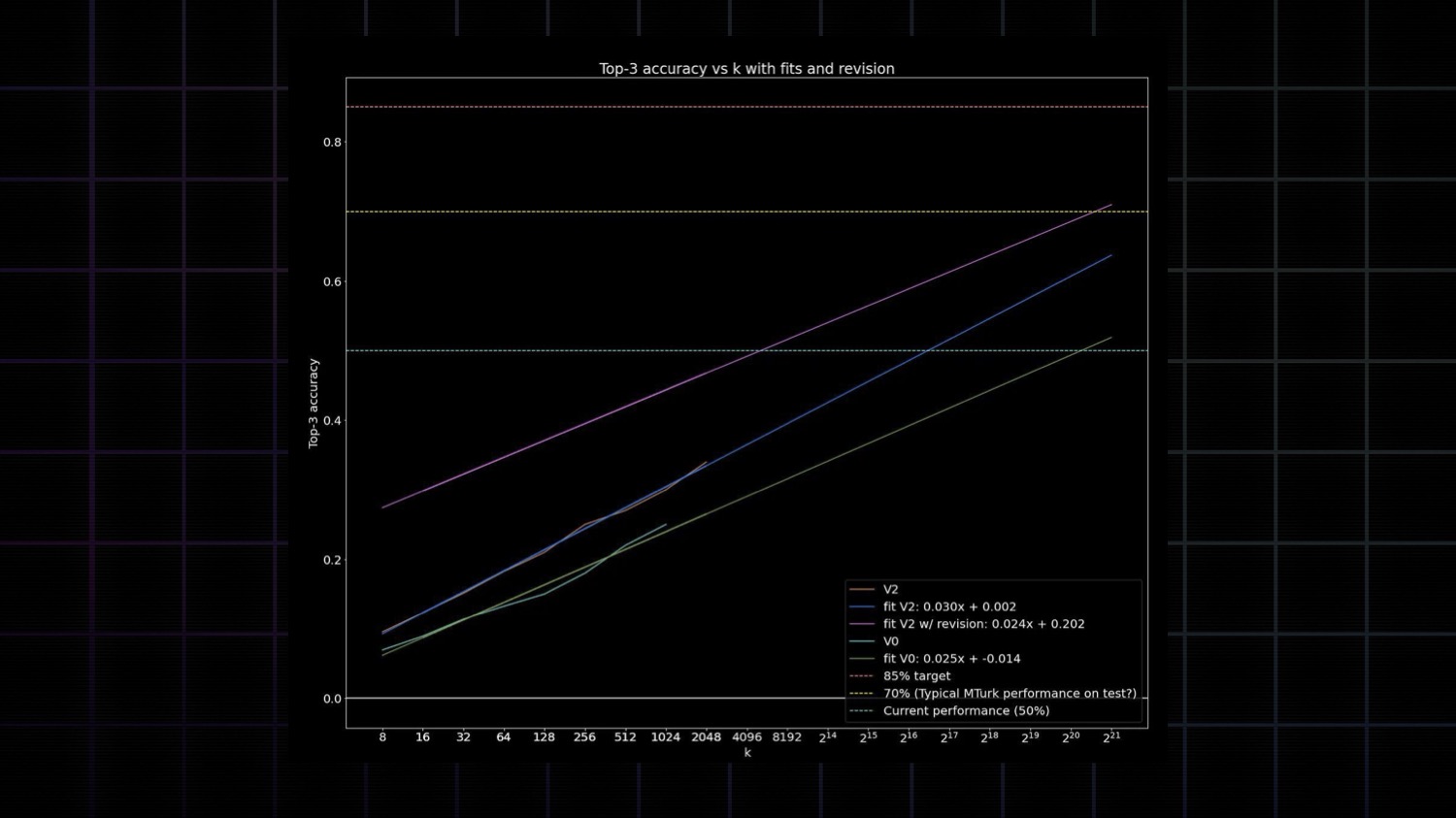
This solution, coded by Ryan Greenblatt, scored 43% by having GPT-4o generate k=2,048 solution programs per task and deterministically verifying them against the task demonstrations. Then he assessed how accuracy varied for different values of k, and found the same log-linear relationship between "searching more solution programs" and accuracy.
Fundamentally, you see exponential scaling curves anywhere brute force search is applied. It's O(x^n) complexity.
To beat ARC-AGI this way, you'd need to generate over 100+ million solution programs per task. And, yes, you could actually do this with a sufficiently large datacenter. Would that be AGI? Not quite.
Back in 2020, before any LLMs, an ensemble of hard-coded DSL and brute force search were able to beat nearly 50% of ARC tasks.
Practicality rules out O(x^n) search for scaled up AI systems. And more importantly, efficiency matters for intelligence. In fact, it is a hallmark and may have even been the gradient of evolution which early organisms climbed to better navigate their environment, find food, and avoid getting eaten.
Consider when you are doing ARC tasks. You "see" a couple potential solutions. And then deterministically check them in your head.
What you’re not doing is generating and testing millions of programs.
o1 does represent a paradigm shift from "memorize the answers" to "memorize the reasoning", but is not a departure from the broader paradigm of improving model accuracy by putting more things into the pre-training distribution.
So if LLMs can't beat ARC, o1 can't beat ARC, and all the existing frontier AI approaches can't beat ARC, what could?
François Chollet
There's been lots of talk about how LLMs perform "in-context learning" to adapt to new problems. But what seems to actually happen is that LLMs are fetching memorized programs that map to the current prompt.
If they don't have a memorized program ready – if they're faced with something slightly unfamiliar, no matter how simple – they will fail. Even when the novelty comes in the form of a small variation of a problem they did memorize.
There are countless examples of this besides ARC-AGI itself.
Here's one. LLMs can solve a Caesar cipher - a basic form of encryption where you are moving the index of a letter by a fixed position. That is very impressive. But, they can only solve it for specific values of the key size – the specific values that are commonly found in examples of Caesar ciphers online.
Pick an unusual value and the model breaks down. That shows that the model has no general understanding of a Caesar cipher and no ability to adapt to slight deviations compared to what they've memorized.
Another example is "Alice in Wonderland" type problems. Questions of the form: "Alice has N brothers and M sisters. How many sisters does Alice's brother have?"
The answer is obviously M + 1 – M plus alice herself. LLMs have no trouble answering this for common values of M and N. But they break down if you use unfamiliar values.
My hypothesis is that LLM performance depends purely on task familiarity. You can make a LLM do anything as long as you give it the opportunity to memorize the solution.
But it cannot adapt to the slightest amount of novelty, even if the novel problem is extremely simple, like in the case of ARC-AGI.
In fact, this is not just LLMs. This is an intrinsic limitation of the curve-fitting paradigm. Of all deep learning.
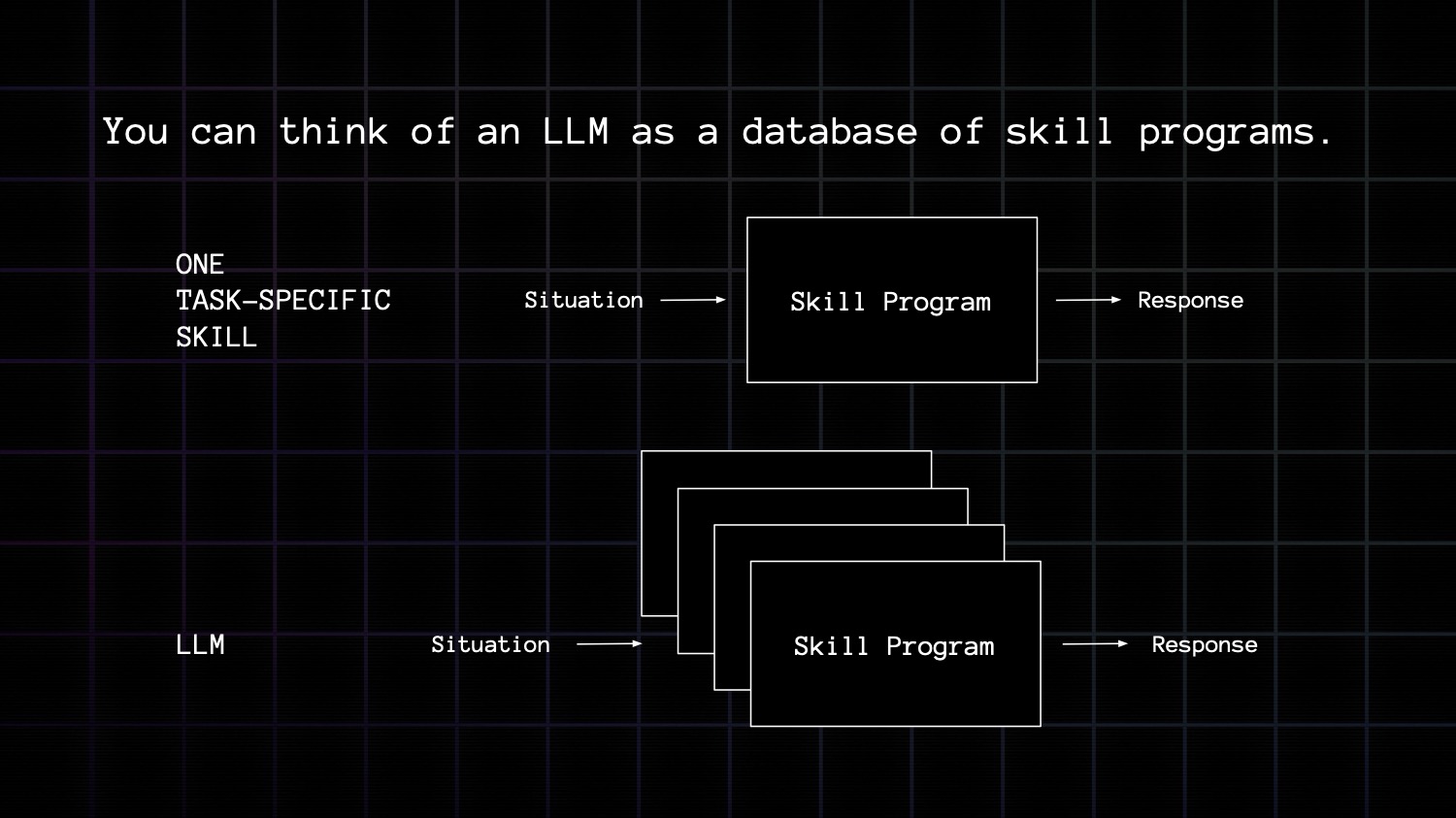
You can think of an LLM, or really any deep learning model, as a database of skill programs. A skill program is just a function mapping a set of situations with the appropriate response. An LLM is just that - covering many skills and many situations.
They're trained to predict what's next given a token sequence. So, they're trained to come up with vector functions, or programs, that map patterns of input tokens to patterns of output tokens.
If LLM had infinite memorization capacity, they would encode these programs via a kind of lookup table from inputs to outputs. But they don't. They only have so many parameters. And as a result they're forced to compress the space of programs they memorize, by expressing new programs in terms of bits and piece of old programs.
This is what forces LLMs to generalize a little bit. This is what makes them useful.
Any time you prompt an LLM your prompt is like a database query that retrieves one or more such program and applies it to your input.
This perfectly explains scaling laws! If you measure model performance based on the score you get on exam-style benchmarks where the skill programs required can be memorized in advance, then performance increases as a function of number of tasks memorized,that is to say, as a function of training data size and parameter count.
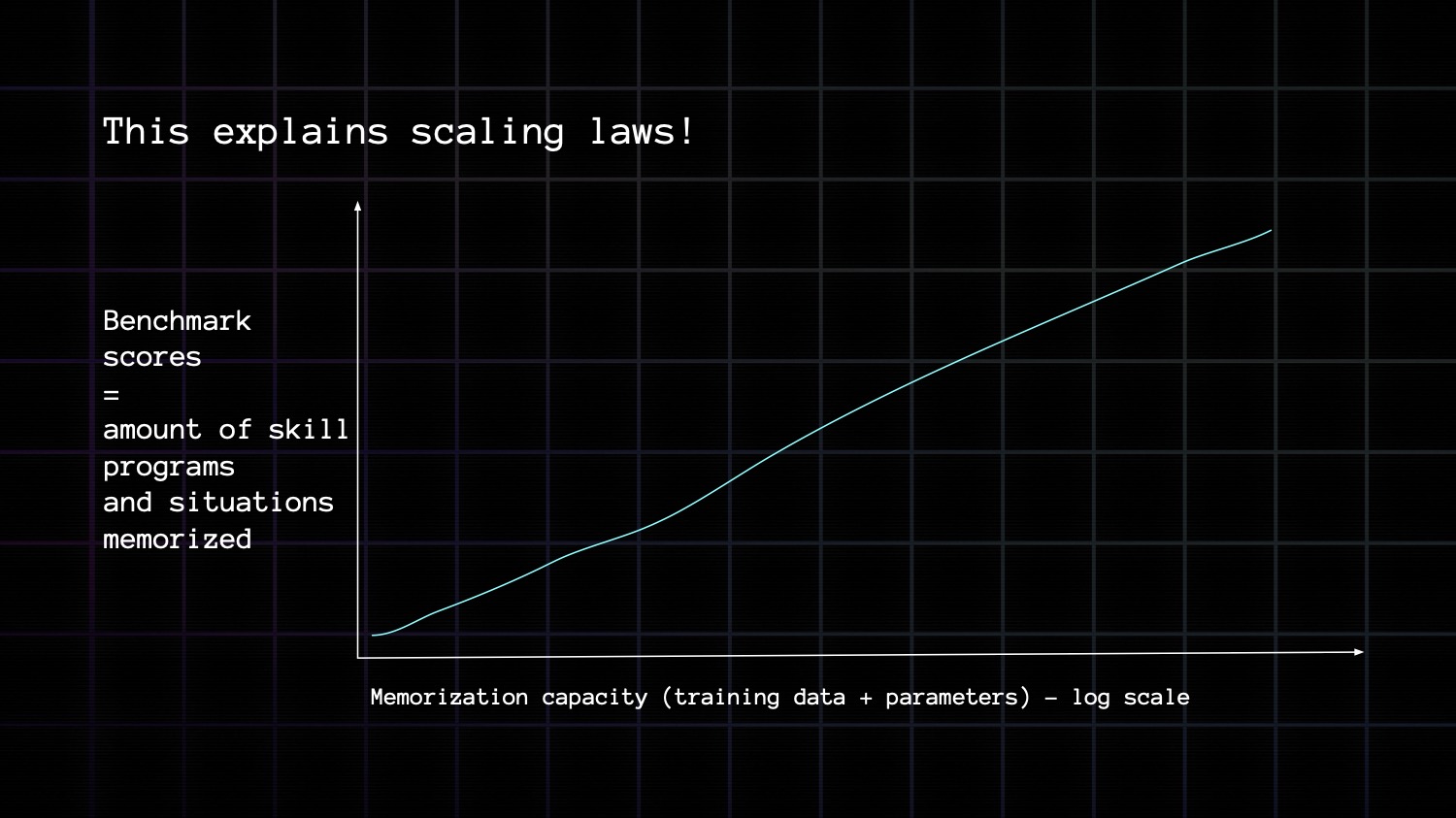
But intelligence cannot be reduced to memorizing every possible task and situation you might ever encounter.
Key concepts of intelligence.
Here are some key concepts you have to take into account if you want to define and measure intelligence.
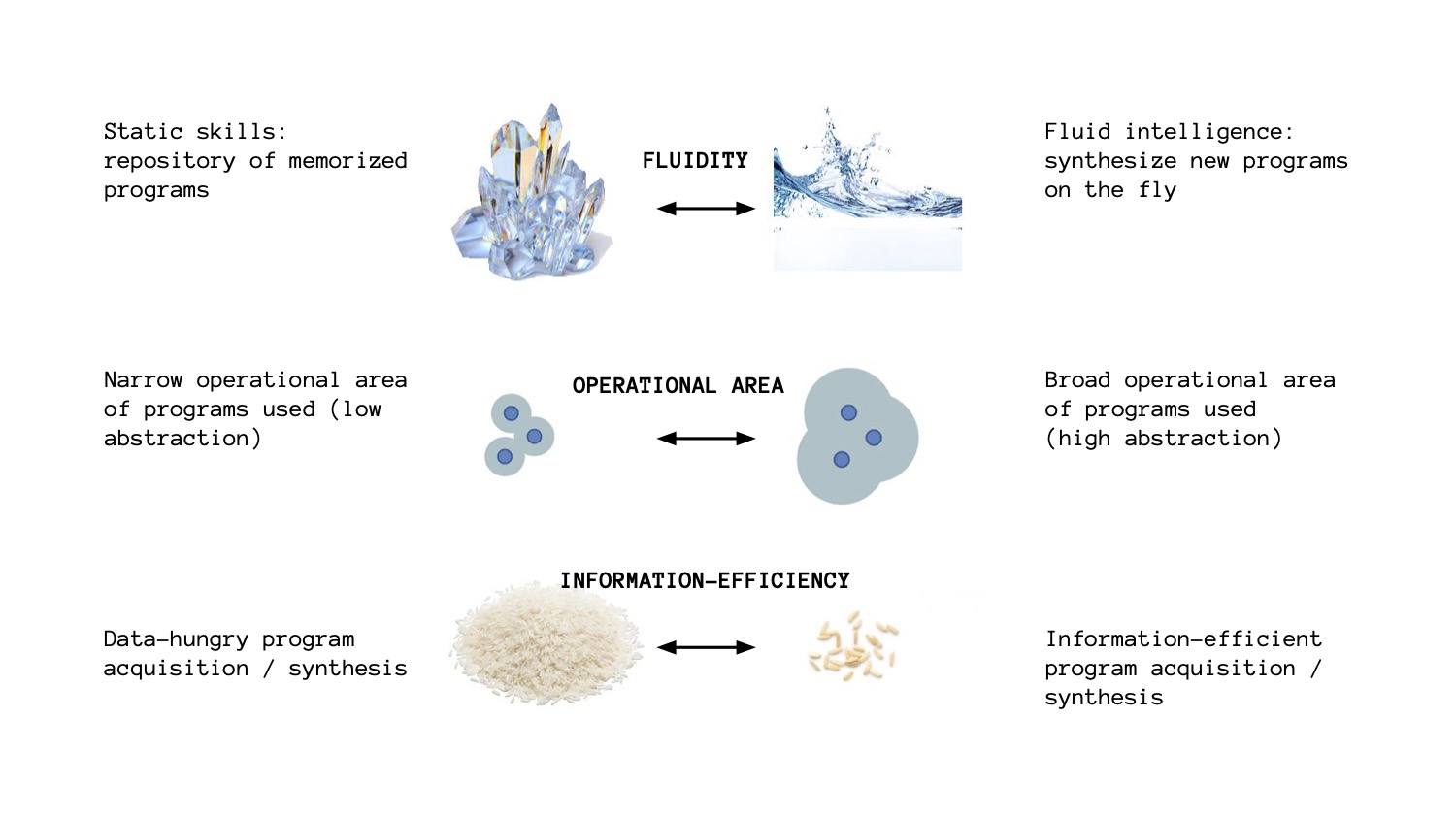
The first thing to keep in mind is the distinction between static skills and fluid intelligence, between having access to a collection of static programs to solve known problems, versus being able to synthesize brand new programs on the fly to face a problem you've never seen before. Mind you, there's a spectrum between the two, it's not one or the other.
The second concept is operational area of the skill programs you have. There's a big difference between being skilled only in situations that are very close to what you're familiar with and being skilled in any situation within a broad scope. For instance, if you know how to add numbers, then you should be able to add any numbers, not just numbers you've seen before. If you know how to drive you should be able to drive in any city, not strictly in a specific geofenced area.
Lastly, we should look at information efficiency. How much information, how much data was required for a system to acquire a new skill program? Higher information efficiency means higher intelligence.
The big takeaway I want you to remember is that skill is not intelligence. Skill and intelligence are separate concepts.
Displaying skill at any number of task does not show intelligence. It's always possible to be skillful at any given task without requiring intelligence. You just need a big lookup table.
This is like the difference between a road network and a road building company. If you have a road network, you can go from A to B for a very specific predefined set of As and Bs. But if you have a road building company, you can start connecting arbitrary As and Bs on the fly, as you needs evolve.
Attributing "intelligence" to a crystallized behavior program is a category error. You are confusing the process and its output.
Intelligence is the ability to deal with new situations. The ability to blaze fresh trails and build new roads.
Don't confuse the trail with the process that created it.
Gradient of Intelligence
I want to make more intelligent machines – Machines that have the ability to turn data into models, on their own, efficiently.
And on one really important thing to understand about model building ability is that it's a spectrum that goes from weak abstraction to strong abstraction, and, thus, strong generalization and high intelligence.
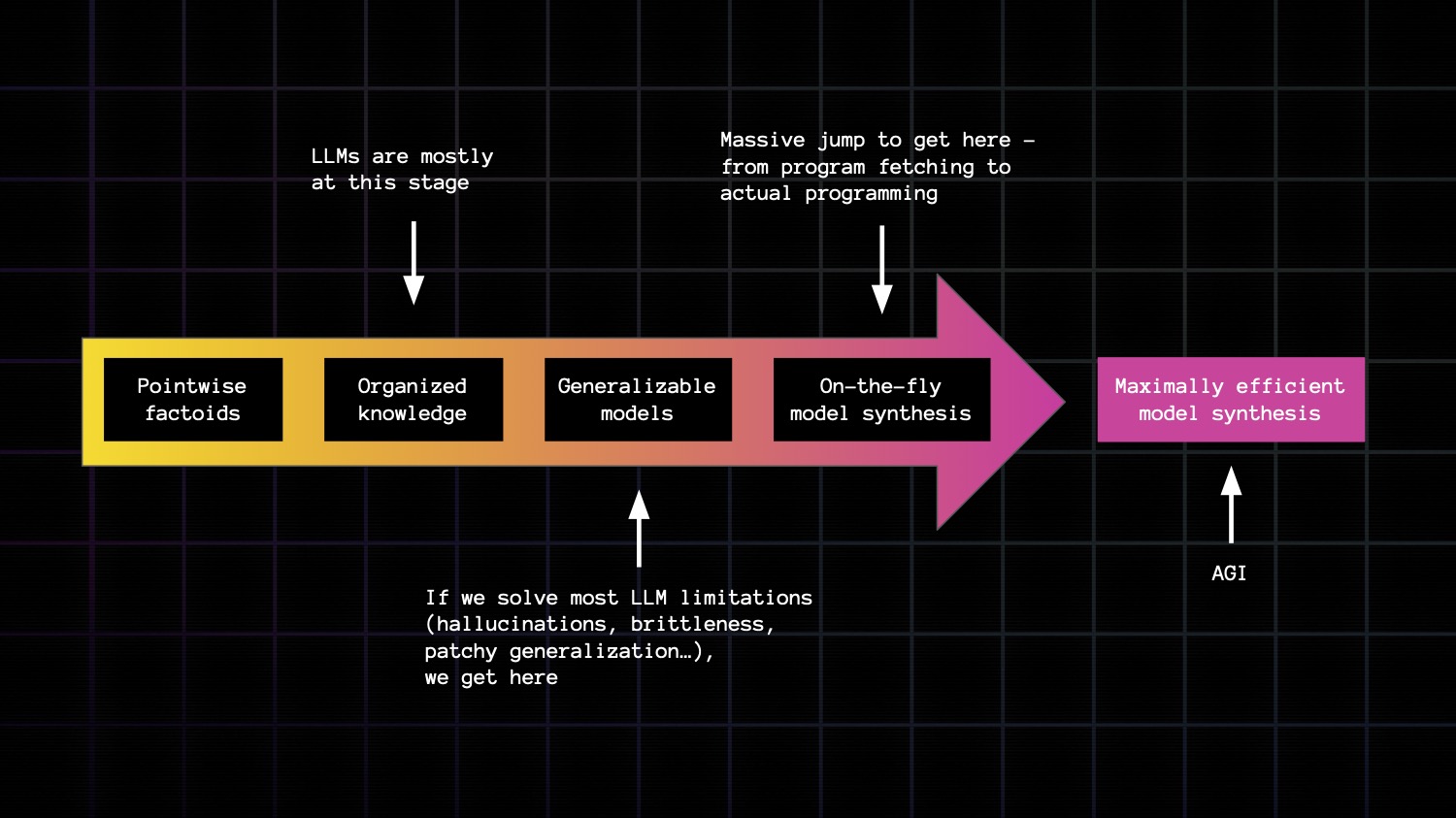
There is a spectrum from factoids to organized knowledge, to abstract models that can generalize broadly and accurately, to meta models that enable you to generate new models on the fly to fit a given situation.
The degree zero here is when you purely memorize pointwise factoids. There's no abstraction involved and it doesn't generalize at all past what you memorized.
Here we represent our factoids as functions. These functions take no arguments, which is how you know they're not abstract.
Once you have lots of related factoids, you can organize them into into abstract functions which encode knowledge.
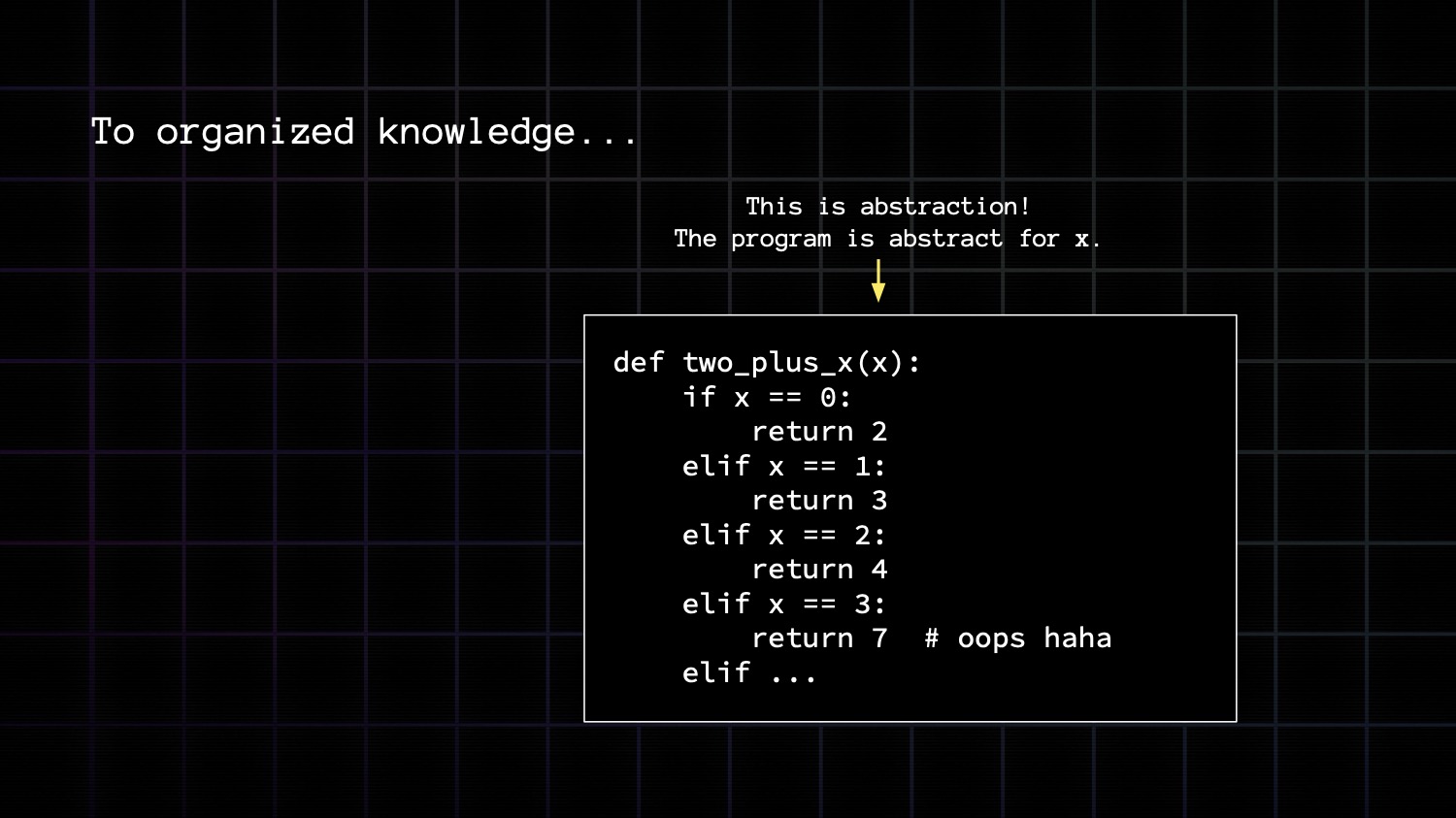
You can tell this program here is abstract because it takes a variable, x. It is abstract for x.
Curve-fitting is good at this kind of knowledge organization and interpolation, but the thing with this type of organized knowledge based on pointwise factoids or interpolating between pointwise factoids is that it doesn't generalize that well. It looks like abstraction, but it's relatively weak abstraction. It may be inaccurate. It may not work on data points that are far from what you've seen before.
The next degree is to turn your knowledge into abstract models.
A model doesn't encode factoids anymore, or interpolation between factoids, it encodes a concise way of processing your inputs to obtain the desired result.
Here for instance, our model of addition is an algorithm expressed in terms of binary operators. A model of this kind will generalize strongly. It will be able to return the right answer. The exactly right answer. For any input at all even inputs very far from the distribution of inputs that your agent may have seen before. That is strong abstraction. This is where LLMs still fall short.
The next stage is the ability to generate abstraction autonomously. This is how you're going to be able to handle novel problems, problems you haven't been prepared for. This is what intelligence is, as opposed to knowledge and crystallized skills.
The last stage is to be able to do so in a way that is maximally information efficient. This means you should be able to master new tasks using very little experience, very little information about the task. Not only are you going to display high skill at the task, meaning that the model you're applying can generalize strongly, but you will only have to look at a few examples, a few situations, to produce that model. This is AGI. We're pretty far from it.
If you want to situate LLMs on the spectrum of abstraction, they're somewhere between organized knowledge and generalizable models. They're clearly not quite at the model stage. If they were at the model stage they could actually add numbers together reliably, or solve "Alice in Wonderland" problems.
But they do have a lot of knowledge and that knowledge is compressed and structured in such a way that it can generalize to some distance from previously seen situations. It's not just lots of pointwise factoids.
If we solve all the problems that LLMs have today we'll get one stage ahead to reliable models that generalize.
But to get to autonomous model generation we will need a massive jump. You cannot purely scale the current approach and get there. You have to change direction. And AGI is still a very long way off after that.
So, concretely, how do we make machines that can autonomously produce their own models, on the fly?
The answer is abstraction. Abstraction is the engine of generalization. It's the engine of modeling. Abstraction is how you turn observations into models that will generalize to new situations.
At a high level, abstraction is about analogy making. It is sensitivity to analogies. If you have a high sensitivity to analogies, you will extract powerful abstractions from little experience, and you will be able to use these abstractions to operate in a maximally large area of future experience space.
Crucially, there's more than one way to draw analogies. There are exactly two ways. This is important.
There are 2 key categories of analogies from which arise 2 categories of abstraction: value-centric abstraction, and program-centric abstraction.
They're pretty similar to each other. They mirror each other. Both are about comparing things and merging individual instances into common abstractions by eliminating certain details about these instances. You take a bunch of things, you compare them, you drop the details that don't matter, and what you're left with is an abstraction.
But the key difference between the two is one operates over a continuous domain and the other operates over a discrete domain.
Value-centric abstraction is about comparing things via a continuous distance function. It's what powers human perception, intuition, pattern recognition
Meanwhile program-centric abstraction is about comparing discrete programs, which is to say graphs, and rather than computing distances you're looking for exact subgraph isomorphisms. It's similar to human reasoning, and it's what software engineers do. If you hear a software engineer talk about abstraction, they're talking about this.
Both forms of abstraction are driven by analogy making. Analogy is the fundamental engine that produces abstraction.
Value analogy is geometrically grounded: you compare instances via a distance function and you create abstractions by merging instances that are similar into a prototype.
Program analogy is topologically grounded: you compare the structure of two graphs and you create abstraction by merging instances that are isomorphic into an abstract program.
All cognition arises from a combination of these 2 forms of abstraction.
You can remember them via the left brain vs right brain metaphor. One half is for perception/intuition/modern ML. The other half represents reasoning, planning, and mathematics. It also mirrors the System 1 thinking vs System 2 thinking distinction from Daniel Kahneman.
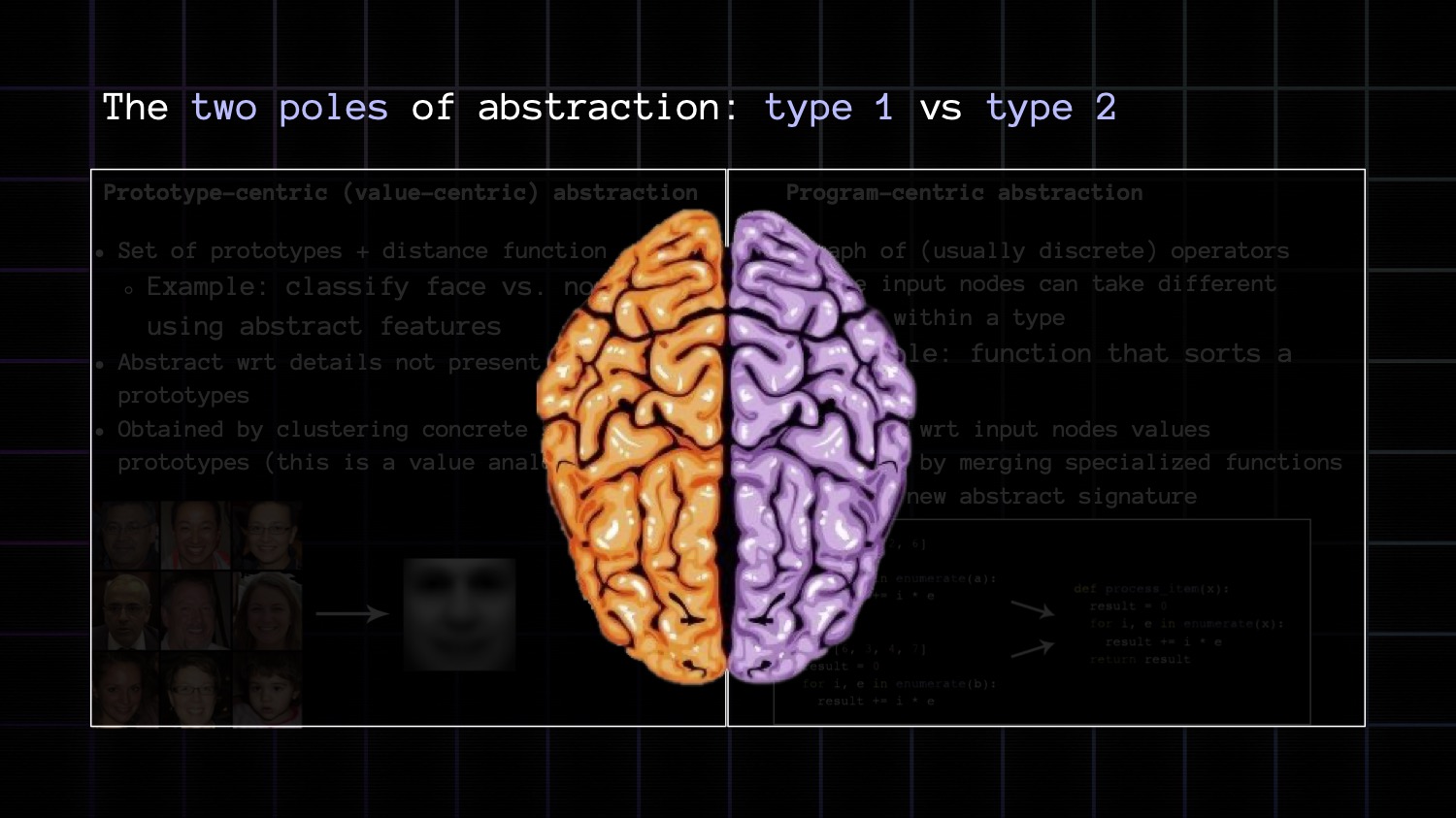
This is a metaphor, mind you. This is not literally how the brain works.
Transformers are great at type 1 abstraction. They can do everything that type 1 is effective for – perception, intuition, and pattern recognition. In that sense they represent a major breakthrough in AI. But they're not a good fit for type 2 abstraction and this is where all the limitations that we listed come from. This is why you cannot add numbers with a Transformer even one trained on all the data on the Internet.
Get to Type 2
So how do you go forward from here? How do we get to type 2?
The answer is that you have to leverage discrete program search as opposed to purely manipulating continuous and interpolative embedding spaces learned with gradient descent. That's an entirely separate branch of computer science compared to ML, and we have to merge it with modern ML to get to general AI.
What's "discrete program search"? It's combinatorial search over graphs of operators taken from a domain-specific language, or a DSL.
To better understand it, you can draw an analogy between machine learning and program synthesis.
In ML, your model is a differentiable parametric function; in program synthesis, it's a graph of ops from a domain specific language (a DSL).
In ML, your learning engine is GD. In PS, it's combinatorial search.
In ML, the key obstacle is that you need a dense sampling of your problem manifold, you need a ton of data. In PS, the key challenge is combinatorial explosion.
You can use PS to solve problems form very, very few examples, but the set of possible programs you can build grows combinatorially with program size.
When I launched the first ARC-AGI competition in 2020, I predicted that the winning entries would use Program synthesis. And in fact, they all did. The winner scored 19% using brute force program search. Today, refined versions of this very basic approach do up to 36%. We know that up to at least 50% is feasible without even using anything smarter than brute force program search.
Meanwhile, LLM-based approaches only started taking off this year. Previously, GPT-3 scored 0%. Today, o1 and Claude 3.5 sonnet score 21% on the public leaderboard.
The top entries on the public and private leaderboard are using a combination of LLMs and search – the state of the art is around 40 to 50% at this time.
So discrete program search has already proven to be a powerful tool to approach this kind of problem. LLMs are also starting to show strong results. Where do we go next?
I said earlier that all intelligence is a combination of two forms of abstraction, type 1 and type 2. I don't think you can go very far with only of these, you need to combine the two to achieve their true potential. And that's what human intelligence is really good at. That's what makes humans special. We combine perception & intuition together with explicit step by step reasoning. We combine both forms of abstraction.
For instance, when you play chess, you're using type 2 when you calculate, when you unfold some potential moves, step by step. But you're not doing this for every possible move – there are lots of them. You're only doing it for a couple of different options. The way you narrow down these options is via intuition based on pattern recognition, which you build up through experience. That's type 1. So you use type 1 intuition to make type 2 calculation tractable.
So how does it work?
The key system 2 technique is discrete search over a space of programs. The blocker that you run into is combinatorial explosion. Meanwhile, the key system 1 technique is curve fitting and interpolation; you embed a lot of data into an interpolative manifold that enables fast but approximate judgement calls about the target space.
The big idea is to leverage those fast, but approximate judgements calls to fight combinatorial explosion. Use them as a form of intuition about the structure of the program space that you're trying to search over, so as to make search tractable.
A simple analogy to understand this is drawing a map.
You take a space of discrete objects with discrete relationships that would normally require combinatorial search, like pathfinding in the Paris metro. And you embed them into a geometric manifold where you can use a continuous distance function to make fast, but approximate guesses about discrete relationships like directions, distance, and pathfinding. This enables you to keep combinatorial explosion in check.
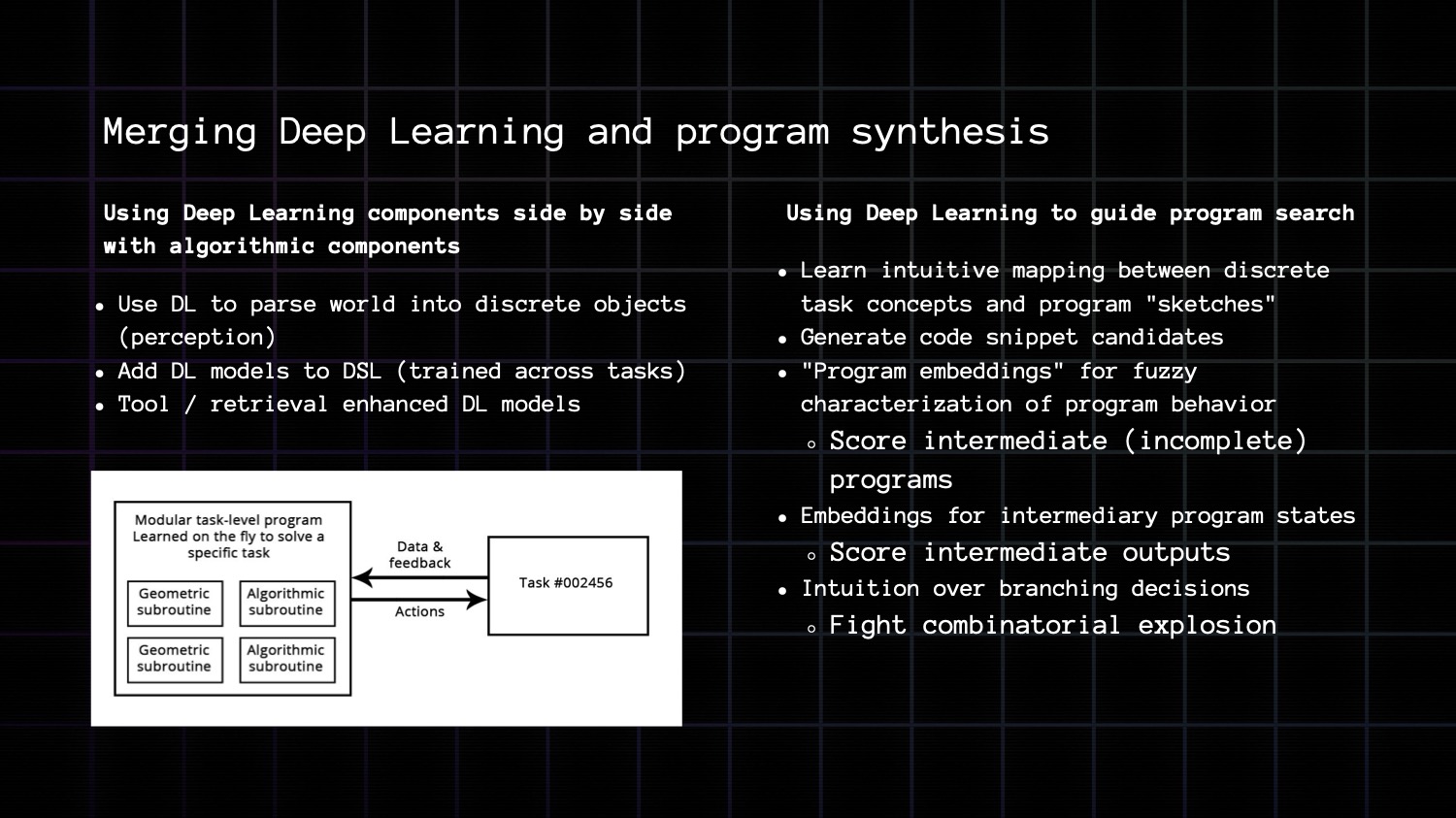
Here are two exciting research areas to combine the strength of DL with the strength of program synthesis.
- Discrete programs that incorporate deep learning components. Use DL as a perception layer to parse a situation into discrete building blocks that you can feed to a program synthesis engine, or add symbolic addons to your DL model.
- Deep learning models that inform discrete search and improve its efficiency. Use DL as a driver or guide for program synthesis it will give you intuitive program sketches to guide your search. It will reduce the space of possible branching decisions that you should consider over each node.
What would that look like in the context of ARC-AGI? I'm going to spell out to you how you can crack ARC-AGI and win a million dollars!
There are two directions you can go.
You can use DL to "draw a map" of state space – grid space. In the limit this solves program synthesis. Here's how.
You take your initial state, you look at the corresponding embedding, you take the final target state, you look at its embedding, and then you draw a line on the manifold between input and target. Then you look at the discrete grid states that the line hits. That series of discrete grid states corresponds approximately to the series of transformations to go from input to output. It gives you an approximate program to solve the input -> output mapping.
The other direction you can go is program embedding. You can use DL to draw a map of program space this time. And use this map to make your discrete program search process efficient.
Right now we've only started scratching the surface in terms of exploring these ideas. I strongly believe that within a few years, we're going to crack ARC-AGI, and the solution will be built directly on top of these ideas.
Maybe by one of you!
Mike Knoop
We're still looking for the person or team to beat ARC-AGI. Even though we’ve made progress on SOTA this year, conceptual progress has been limited.
The solution to ARC Prize is going to come from an outsider. Not a commercial lab training massive models. In fact, my personal belief is ARC can be beaten with a 7B model and <10k LOC.
It’s very possible that one of you reading this might be able to crack AGI.
The ARC Prize 2024 contest ends Nov 10, but we don’t expect to have a Grand Prize winner this year. We are going to keep running ARC Prize every year until someone beats it.
We also have progress prizes. At the end of 2024 we’re going to pay out $50k to the top 5 teams, and $75k to the top 3 conceptual progress papers.
Winners get announced early December and all the newly open-sourced frontier AGI code will be presented at NeurIPS 2024.
Hope to see you on the leaderboard!
